Problema 39
Demostreu que si a, b són els costats d’un triangle 
i l la bisectriu de
l’angle que formen els dos costats i a’, b’ els segments amb quč la bisectriu
divideix el costat c, aleshores, 
.
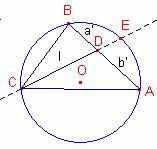Solució:
Considerem la circumferčncia circumscrita al triangle .
Siga D la
intersecció de la bisectriu al včrtex C i el costat oposat.
Siga E la
intersecció de la bisectriu i la circumferčncia circumscrita al triangle.
Els triangle 
, 
són semblants (tenen
els angles iguals).
Aplicant el teorema de Tales:
, per tant, 
, 
(1)
Aplicant la potčncia del punt D respecte de la
circumferčncia circumscrita al triangle:
, és a dir, 
(2)
Substituint (2) en (1):
.
Amb Cabri:
Figura problema039.fig
Applet created on 22/04/06 by Ricard Peiró with CabriJava