Problema 42
En un triangle isòsceles 
, 
està circumscrita una
circumferència.
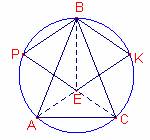
Les continuacions de les bisectrius dels vèrtexs A, C
tallen la circumferència en els punts K i P, respectivament i entre si en el punt
E.
Demostreu que el quadrilàter BKEP és un rombe.
Solució:
Per ser 
bisectrius d’angles
iguals tenim que els arcs PB i KB són iguals, aleshores, 
.
Notem que E és l’incentre del
triangle .
Considerem
l’angle 
.
Per ser un angle inscrit a la circumferència, 
.
Considerem l’angle 
.
Per ser un angle interior a la circumferència, 
.
Per tant el triangle 
és isòsceles,
aleshores, 
.
Anàlogament, 
.
Aleshores el quadrilàter BKEP és un rombe.
Amb Cabri:
Figuraproblema042.fig
Applet created on 22/04/06 by Ricard Peiró with CabriJava