Cabri 3D
Problemes
de geometria per a segon de Batxillerat.
Problema
1:
Determineu
l’equació del plànol que passa pel punt 
i té vector normal o
característic és 
.
Problema
2
Donats
els punts 
, 
.
Determineu
l’equació del plànol que passa pel punt M i és perpendicular al vector 
.
Problema
3
Determineu
l’equació del plànol que passa pels punts 
, 
i és paral·lel al
vector 
.
Problema
4
Determineu
l’equació del plànol que passa pels punts 
, 
, 
.
Problema
5:
Determineu
el punt projecció de 
sobre el plànol que
passa pels punts 
, 
, 
.
Calculeu
la distància entre el punt P i el plànol anterior.
Problema
6
Donats
els punts 
, 
, 
, 
. Calculeu:
a)
El volum del tetraedre ABCD.
b)
L’àrea total del tetraedre.
c)
L’altura sobre la cara 
.
Problema
7
Determineu
el punt Q simètric del punt 
respecte de la recta
que passa pels punts 
, 
.
Problema
8
Donats
els punts 
, 
, 
, determineu:
a)
El vèrtex D el paral·lelogram ABCD.
b)
La mesura dels costats del paral·lelogram ABCD.
c)
L’àrea del paral·lelogram ABCD.
d)
Els angles del paral·lelogram ABCD.
Problema
9
Donats
els punts 
, 
i el vector 
. Determineu:
a)
L’equació general de la recta r que passa pel punt P i té direcció v.
b)
L’equació general del plànol que passa pel punt P i conté la recta r.
c)
La distància del punt A a la recta r.
Problema
10
Es
donen els punts 
i 
, i la recta r d’equació 
.
Es
demana que calculeu raonadament:
a)
El punt C de r que equidista de A i B.
b)
L’àrea del triangle .
Selectivitat
València juny 2008
Problema
11
Siga
la recta r que passa pels punts 
i 
.
Siga
la recta s que passa pels punts 
i 
.
Determineu
la posició relativa de r i s.
Calculeu
la distància entre les rectes r i s.
Problema
12
Les
bases d’un paral·lelepípede són ABCD i EFGH on , 
, 
, 
.
a)
Determineu les coordenades de D, F, G, H.
b)
Calculeu el volum del paral·lelepípede.
c)
Calculeu l’altura del paral·lelepípede sobre la base ABCD.
Solucions cg3
Solucions analítiques
Altres
problemes.
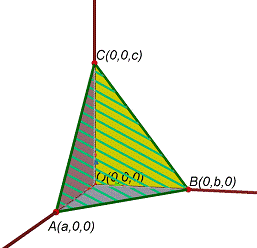
Problema
1
Considerem
el sistema de referència afí 
Siguen
els punts 
, 
, 
.
Siguen
les àrees: 
, 
, 
, 
.
Proveu
que 
.
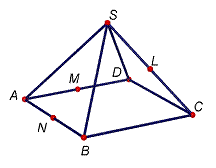
Problema
2
Les
arestes de la piràmide quadrangular ABCDS regular són totes iguals a a.
Siguem
L, M, N els punts migs de les arestes 
, 
i 
, respectivament.
Calculeu
l’àrea del la secció de la piràmide determinada pel plànol que passa pels punts
M, N, L.
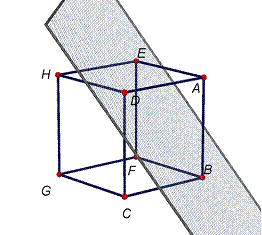
Problema
3
El
cub sòlid de la figura es talla per un plànol que passa pels tres vèrtexs veïns
del vèrtex A, és a dir, D, E, i B.
De
manera semblant, el cub es talla per plànols que passen pels vèrtexs veïns a
cadascun dels set vèrtexs que queden.
Quina
és la figura que queda després de tallar-lo?
Proves
Cangur 2013. Nivell 4, problema 23
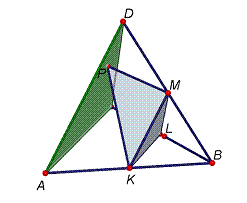Problema 4:
Siga
el tetraedre regular ABCD.
Siguen
K, L, M els punts migs de les arestes AB, BC, BD, respectivament.
Siga
P un punt qualsevol de la cara ACD.
Calculeu
la proporció entre els volums dels tetraedres ABCD i KLMP
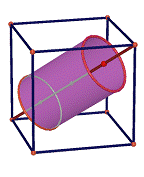
Problema
5:
Determineu
les dimensions d’un cilindre de volum màxim inscrit en un cub
d’aresta
a tal que l’eix del cilindre siga una diagonal del cub.
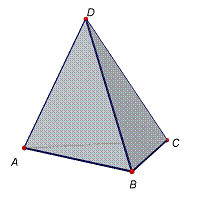Problema 6:
Un
tetraedre està format per dos triangles equilàters de costat a i dos triangles
rectangles isòsceles.
Calculeu
l’àrea i el volum.
Problema
7:
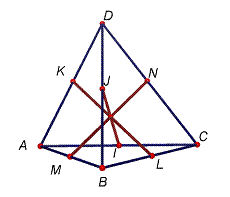En un
tetraedre la suma dels quadrats de les arestes és quatre vegades la suma dels
quadrats dels
segments
que uneixen els punts migs de les arestes oposades.
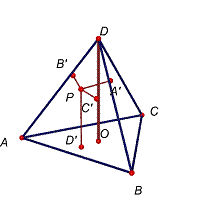
Problema 8
La
suma de distàncies d’un punt interior d’un tetraedre regular a les cares és
igual a l’altura del tetraedre.
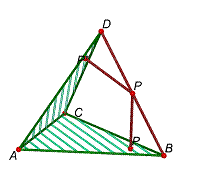Problema 9
Si
un tetraedre té dues cares simètriques respecte d’un plànol que passa per
l’aresta comuna, la suma de les perpendiculars
traçades
a aquestes des d’un punt de l’aresta oposada a l’aresta comuna és constant.
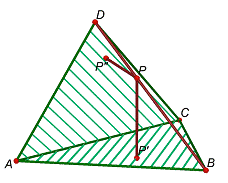
Problema 10
Si
un tetraedre té dues cares iguals, la suma de les perpendiculars traçades a
aquestes des d’un punt
de
l’aresta oposada a l’aresta comuna és constant.
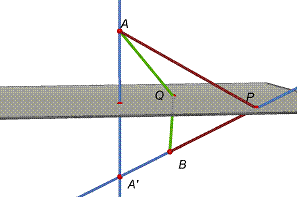Problema 11
Donat un plànol i dos punts A, B
exteriors situats en distinta regió respecte del plànol,
determineu un punt P del plànol
tal que la diferencia de les distàncies a A i B siga máxima.
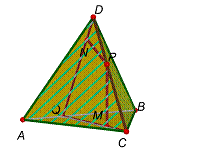
Problema 12
Si un
tetraedre té dues cares iguals, la suma de les perpendiculars traçades a
aquestes cares des d’un punt
de
l’aresta oposada a la comuna a les dues cares és constant.
Cub d’una suma:
