Corbes a partir de definicions geomètriques II:
La limaçon (caragol) de Pascal
La cardioide
L’equació cartesiana de la limaçon de Pascal és:
L’equació en forma polar és:
En el cas que 
la corba
s’anomena cardioide.
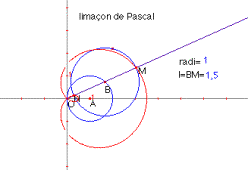Aquesta corba va ser estudiada per primera vegada pel francés Roberval
1630.
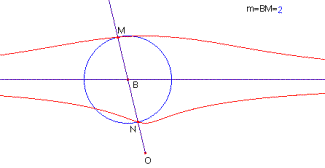
Concoide de Nicomedes
L’equació cartesiana de la concoide de Nicomedes és:
L’equació en forma polar és:
on 
La concoide de Nicomedes (segle II AC) va ser creada per a resoldre el problema de la trisecció de l’angle.
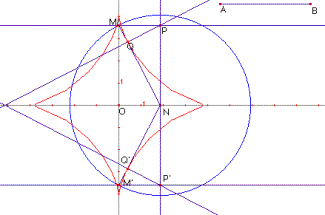
L’astroide
L’equació cartesiana de l’astroide és:
on 
.
 |
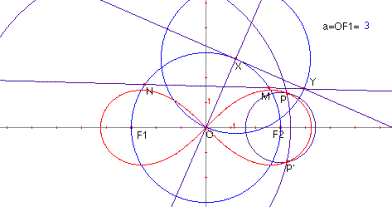
Lemniscata de Bernoulli
Donats els punts 
on 
, el lloc
geomètric dels punts del plànol que el producte de les distàncies a 
són iguals a 
s’anomena lemniscata
de Bernoulli. Donada a conéixer per Jacques Bernoulli en 1694. Les
propietats d’aquesta corba foren estudiades per G. Fagnano (1682-1766) i per
Euler.
L’equació cartesiana de la lemniscata de Bernoulli és:
L’equació en forma polar és:
 |
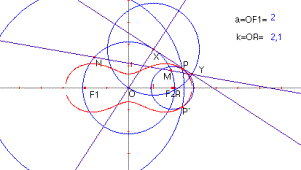
Corba de Cassini.
Donats els punts 
on 
, el lloc
geomètric dels punts del plànol que el producte de les distàncies a 
són iguals a 
s’anomena corba
de Cassini (1680). Aquesta corba és conseqüència dels esforços de
l’astrònom G. Cassini per tal d’entendre els moviments de la Terra al voltant
del Sol.
La corba de Cassini és una generalització de la lemniscata de Bernoulli.
La seua equació
cartesiana és: 
L’equació en forma
polar és: 
 |
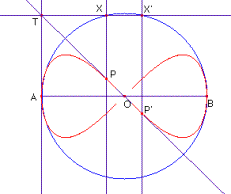
Lemniscata de Geromo
La lemniscata de Geromo.té la següent equació:
, on 
L’equació en forma polar és:
 |