Corbes a partir de definicions geomètriques VI:
La Concoide de Sluse
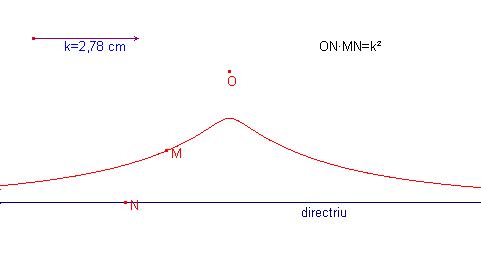
La Concoide de Sluse (matemàtic belga 1622-1685) té per equació en forma polar:
on la directriu té
equació 
i
pol O,
És el lloc geomètric
dels punts M de la recta directriu tals que 
on N recorre tots els punts de la
recta.
L’equació cartesiana és:
 |
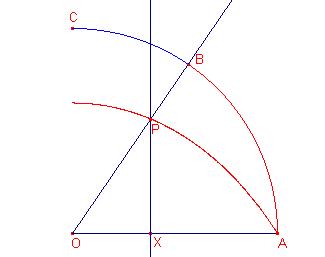
La quadratiu d’Hippias
La quadratiu d’Hippias té per equació polar:
on 
L’equació cartesiana és:
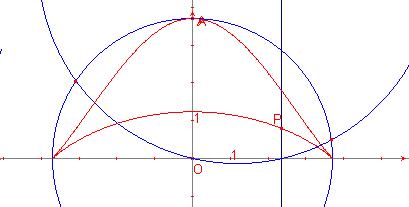
El bicorn.
El bicorn és la corba d’equació cartesiana:
on a=OA
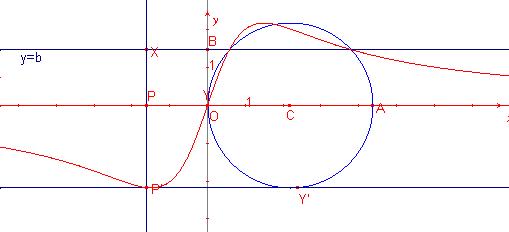
La serpentina.
La serpentina és la corba d’equació polar:
L’equació cartesiana és:
El foli de Descartes.
El foli de Descartes és la corba d’equació cartesiana:
L’equació polar és:
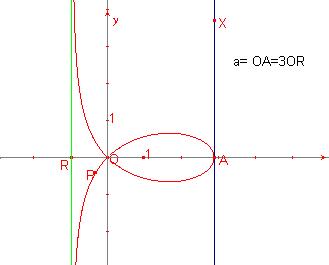
La Corba de Besace.
La corba de Besace té per equació cartesiana:
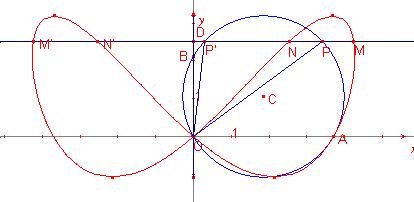
Donat la
circumferència de diàmetre AB, la corba de Besace és el lloc geomètric dels
punts M d’una recta variable r paral·lela a OA tal que 
on P és el punt
intersecció de la circumferència i la recta r.
Nota si B(0,0) la corba és la lemniscata de Geromo.