Corbes a partir de definicions geomètriques IV:
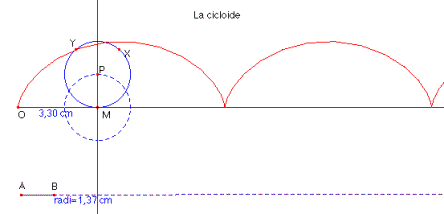
La cicloide
La cicloide és la corba definida pel lloc geomètric de les posicions d’un punt fix d’una circumferència que roda sense relliscar sobre una recta. La recta s’anomena directriu i la circumferència s’anomena ruleta o generatriu.
L’equació paramètrica de la cicloide és:
on 
 |
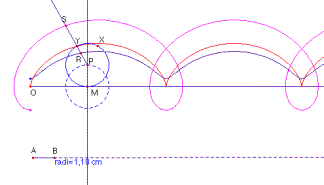
Siga la semirecta d’origen P que passa pel punt Y.
Si considerem el
punt R interior a la circumferència 
. El lloc geomètric del punt R al
variar M sobre la semirecta d s’anomena cicloide acurtada.
Si considerem el
punt S exterior a la circumferència 
. El lloc geomètric del punt S al
variar M sobre la semirecta d s’anomena cicloide allargada.
 |
L’epicicloide
L’epicloide és la corba definida pel lloc geomètric de les posicions d’un punt fix d’una circumferència que roda exteriorment, sense relliscar, sobre una circumferència. La circumferència que roda s’anomena ruleta o generatriu i aquella sobre la qual roda s’anomena circumferència directriu.
L’equació paramètrica de l’epicicloide és:
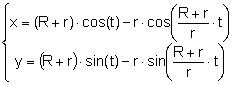on 
 |
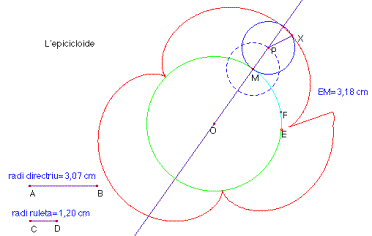Si la proporció entre el radi de la circumferència directriu i el radi de la ruleta és 1:n on n és un nombre natural major o igual que 2 l’epicicloide dibuixa n períodes complets sobre la circumferència directriu.
 |
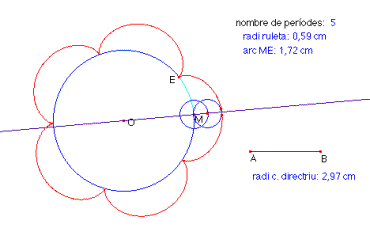Les hipocicloides
La hipocicloide és la corba definida pel lloc geomètric de les posicions d’un punt fix d’una circumferència que roda interiorment, sense relliscar, sobre una circumferència. La circumferència que roda s’anomena ruleta o generatriu i aquella sobre la qual roda s’anomena circumferència directriu.
L’equació paramètrica de la hipocicloide és:
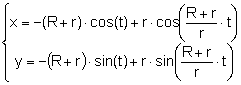on 
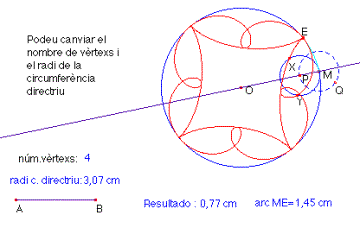
L’astroide és una hipocicloide de 4 períodes.
El deltoide és una hipocicloide de 3 períodes.