|
|
|||||||||||||||||||||||||
|
Teoria: Circumferència i cercle |
|||||||||||||||||||||||||
|
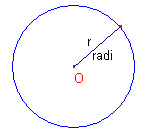
La circumferència és el conjunt de
tots els punts del plànol la distància dels quals a un altre donat del plànol (centre) és constant i
anomenada radi.
El cercle és el conjunt
de tots els punts del plànol la distància dels quals a un altre donat del plànol (centre) és igual o
menor a un segment donat anomenat radi, és a dir, els punts del cercle són els de la circumferència i els interiors
a la circumferència. Altres
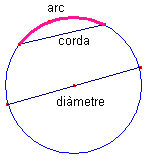
elements d’una circumferència. Corda és el segment
que uneix dos punts de la circumferència. Diàmetre és una corda que
passa pel centre. Arc de circumferència és cadascuna
de les parts en què la corda divideix la circumferència.
Propietats: 1.- La mediatriu a una corda passa pel centre de la
circumferència. 2.- Una recta tangent a una circumferència és perpendicular al
radi que forma el centre de la circumferència i el punt de tangència.
Applet
created on 6/04/11 by Ricard Peiró with CabriJava Longitud de la
circumferència
La longitud de la circumferència i el diàmetre són proporcionals
i la proporció és el nombre real Per tant, Àrea d’un cercle
L’àrea d’un cercle és igual:
Applet
created on 6/04/11 by Ricard Peiró with CabriJava Angles
de la circumferència i la seua mesura. Angle Central S’anomena angle central
ÐAOB, l’angle el vèrtex
del qual és el centre de la circumferència i els seus costats contenen radis. El conjunt del punts de la circumferència interiors a l’angle
s’anomena arc de la circumferència. L’ angle central mesura el mateix que l’arc que abraça.
Applet
created on 6/04/11 by Ricard Peiró with CabriJava Angle inscrit S’anomena angle inscrit
ÐBAC, l’angle el vèrtex
del qual és un punt de la circumferència, i els costats són dues cordes de la mateixa. L’angle inscrit d’una circumferència, mesura la meitat que l’arc
que abraça.
Applet
created on 6/04/11 by Ricard Peiró with CabriJava Angle semiinscrit S’anomena angle
semiinscrit ÐBAC, l’angle el
vèrtex del qual és un punt de la circumferència, un costat és una corda i l’altre costat és tangent a la
circumferència. L’angle semiinscrit mesura la meitat de l’arc de circumferència
que abraça.
Applet
created on 6/04/11 by Ricard Peiró with CabriJava Angle interior S’anomena angle interior
ÐBAC, l’angle el vèrtex
del qual és un punt interior de la circumferència, i els costats són cordes de la circumferència. L’angle interior mesura la semisuma dels arcs que abraça. Angle exterior L’angle interior mesura la semisuma dels arcs que abraça. S’anomena angle exterior ÐBAC, l’angle el vèrtex
del qual és un punt exterior a la circumferència, i els costats són cordes o rectes tangents de la circumferència. L’angle exterior, mesura la semidiferència dels arcs que abraça. Quadrilàters
cíclics. Una quadrilàter és cíclic si es pot inscriure en una
circumferència. Propietat: Un quadrilàter convex és cíclic (inscriptible en una
circumferència) si i només si els seus
angles oposats sumen 180º.
Applet
created on 6/04/11 by Ricard Peiró with CabriJava Teorema de Ptolomeu. Un quadrilàter convex ABCD és cíclic (inscrit en una
circumferència) si i només si la suma dels productes dels costats oposats és igual al producte de les
diagonals
Applet
created on 6/04/11 by Ricard Peiró with CabriJava Quadrilàter
circumscrit a una circumferència. La suma dels costats oposats d’una quadrilàter convex circumscrit
a una circumferència són iguals. Si ABCD és circumscrit a una circumferència:
Applet
created on 6/04/11 by Ricard Peiró with CabriJava Potència d’un punt respecte d’una
circumferència. Teorema: Siga la circumferència C de centre O. Siga P un punt qualsevol
del plànol. Siga la recta r que passa pel punt P, que talla la circumferència
C en els punts A, A’. Siga la recta s que passa pel punt P, que talla la circumferència
C en els punts B, B’. Aleshores: potència del punt P
respecte de la circumferència C. Si P és exterior a la circumferència C tenim que: Si P és interior a la circumferència C tenim que:
Applet
created on 6/04/11 by Ricard Peiró with CabriJava |
|||||||||||||||||||||||||