|
|
|||||||||||||||||||||||||
|
Teoria: Els triangles i les seues propietats |
|||||||||||||||||||||||||
TRIANGLES.
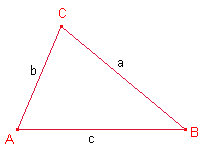
anomenats costats els extrems
dels quals es tallen 2 a 2 en 3 punts anomenats vèrtexs. Els vèrtexs s’escriuen en lletres
majúscules i el costat oposat al vèrtex en la mateixa lletra minúscula. Propietats: 1.- La suma de dos costats és major que l’altre costat.
Applet
created on 5/04/11 byRicard Peiró with CabriJava 2.- La suma dels angles d’un triangle mesura 180º.
Applet
created on 5/04/11 by Ricard Peiró with CabriJava Dos triangles Criteris
d’igualtat de triangles. Criteri 1. Dos triangles dos triangles són iguals si tenen iguals dos costats i l’angle
comprés entre ells. Criteri 2. Dos triangles dos triangles són iguals si tenen igual un costat i els angles
continguts. Criteri 3. Dos triangles dos triangles són iguals si tenen els costats corresponents són
iguals. Classificació
dels triangles: Segons els costats: Equilàter: Té els 3
costats són iguals. Isòsceles: Té 2 costats
iguals. Escalè: Té els tres
costats desiguals. Segons els angles: Acutangle: Té els 3
angles aguts. Rectangle: Té un angle
recte i els altres aguts. Obtusangle: Té un angle
obtús i els altres aguts. Les mitjanes i el baricentre
La mitjana: És
el segment que uneix un vèrtex i el punt mig del costat oposat al vèrtex. Les 3 mitjanes d’un triangle es creuen en un punt G anomenat baricentre o centre de gravetat
del triangle. Propietat
del baricentre d’un triangle. El baricentre d’un triangle està a doble distància del vèrtex que
del punt mig del costat oposat. Mesures de les mitjanes referides als vèrtexs A, B, i C són:
Applet
created on 5/04/11 by Ricard Peiró with CabriJava Les mediatrius i el circumcentre
La mediatriu: És la recta que
passa pel punt mig de cada costat i és perpendicular al costat. Les 3 mediatrius d’un triangle es creuen en un punt que s’anomena
circumcentre, que té la propietat de ser el centre de la circumferència circumscrita al triangle. El diàmetre de la circumferència circumscrita és igual a la
constant de la proporció del teorema dels sinus. Teorema del sinus: En qualsevol triangle
Applet
created on 5/04/11 by Ricard Peiró with CabriJava Les bisectrius interiors i
l’incentre La bisectriu: És la recta que passa pel vèrtex que formen dos costats i divideix per
la meitat a l’angle que formen els mateixos costats. Les 3 bisectrius interiors d’un triangle es
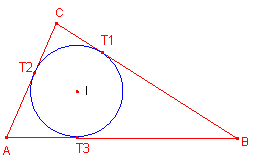
creuen en un punt que s’anomena incentre, que té la propietat de ser el centre de la circumferència
inscrita al triangle. Propietat dels punts de tangència de la circumferència inscrita
al triangle.
Siga Siga Siga Aleshores:
Applet
created on 5/04/11 by Ricard Peiró with CabriJava Propietat de la bisectriu d’un triangle: Siga el triangle Aleshores:
Applet
created on 5/04/11 by Ricard Peiró with CabriJava Les
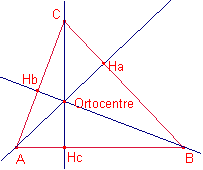
altures i l’ortocentre L’altura: És la recta
que passa per un vèrtex i es perpendicular al costat oposat. Les tres altures d’un triangle es creuen en un punt que s’anomena
ortocentre.
Normalment considerem l’altura d’un triangle
com el segment de la recta altura que uneix el vèrtex i el punt del costat oposat,
En un triangle qualsevol
Applet
created on 5/04/11 by Ricard Peiró with CabriJava Àrea d’un triangle. L’àrea d’un triangle és
La fórmula no depén de la base escollida. Fórmula d’Heró. L’àrea
d’un triangle
Si Fórmula trigonomètrica:
Altres fórmules del càlcul de l’àrea d’un triangle: Si r és el radi de la circumferència inscrita i
Si R és el radi de la circumferència circumscrita:
Propietats
de proporcionalitat de les àrees de dos triangles Dos triangles que tenen la mateixa base les àrees són
proporcionals a les altures.
Applet
created on 6/04/11 by Ricard Peiró with CabriJava Dos triangles que tenen la mateixa altura les àrees són
proporcionals a les bases.
Applet
created on 6/04/11 by Ricard Peiró with CabriJava |
|||||||||||||||||||||||||